
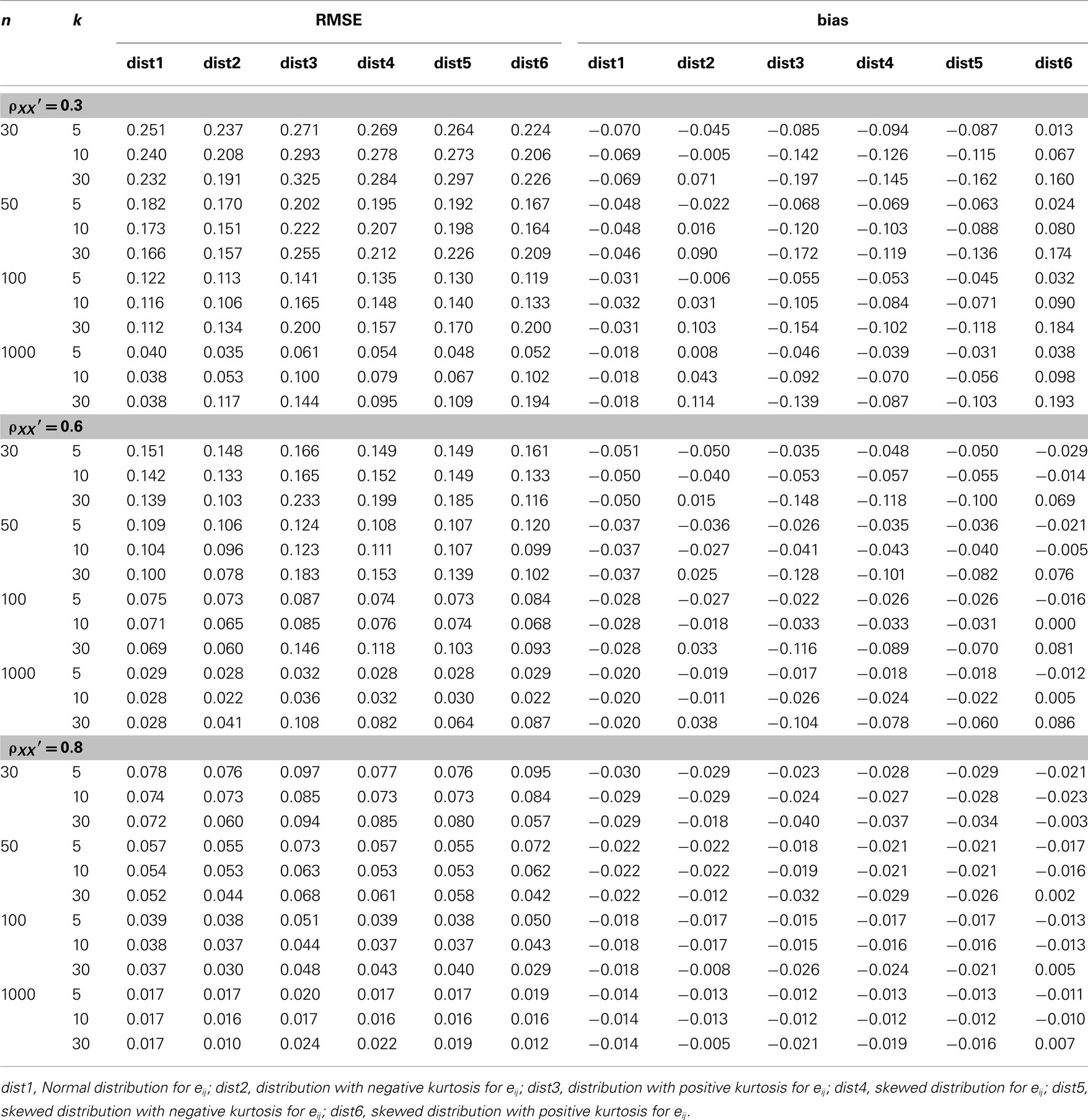
Thus, the probability that a 60 year old man will have a BMI greater than 30 is 43%. You can also calculate the probability that a 60 year old man in this population would have a BMI greater than 30 either from the Z-score or from the mean and standard deviation.

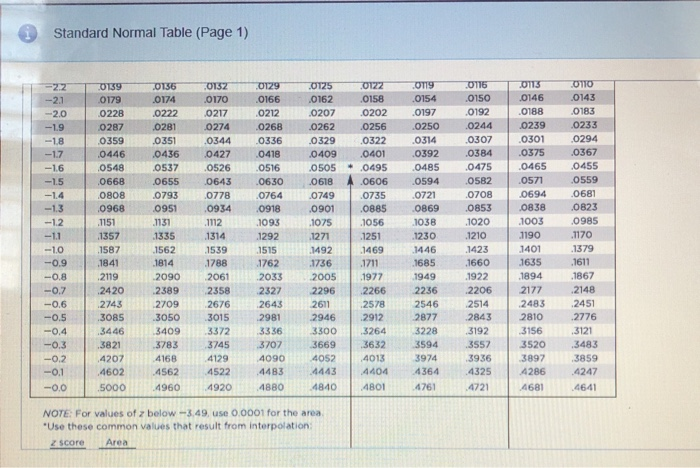
Using the same problem as in the previous example, you can also use R to compute the probabilty directly without computing Z. The probability that a 60 year old man in this population will have a BMI less than 30 is 56.7%. Next, you use R to compute the probability of a Z-score less than 0.17: First, you calculate the Z-score for a BMI of 30: Suppose that BMI measures for men age 60 in the Framingham Heart Study population is normally distributed with a mean (μ) = 29 and standard deviation (σ) = 6. You are asked to compute the probability that a 60 year old man in thispopulation will have a BMI less than 30. If you have compted a Z-score you can find the probability of a Z-score less than that by using pnorm(Z). Keep in mind that the probabilities obtained from tables for the standard normal distribution or pnorm give the area (probability) to the left of that Z-score.Ĭomputing Probabilities from the Standard Normal Distribution pnorm( Z) The illustration below shows the probabilities that would be obtained for selected Z-scores. Once you have computed a Z-score, you can look up the probability in a table for the standard normal distribution or you can use the pnorm() function in R. Z scores above the mean are positive and Z scores below the mean are negative. The mean of the standard normal distribution is 0. Therefore, the 10th percentile of the standard normal distribution is -1.28.Z Scores and the Standard Normal DistributionĪ Z score represents how many standard deviations an observation is away from the mean. We look to the leftmost of the row and up to the top of the column to find the corresponding z-value. We search the body of the tables and find that the closest value to 0.1000 is 0.1003.
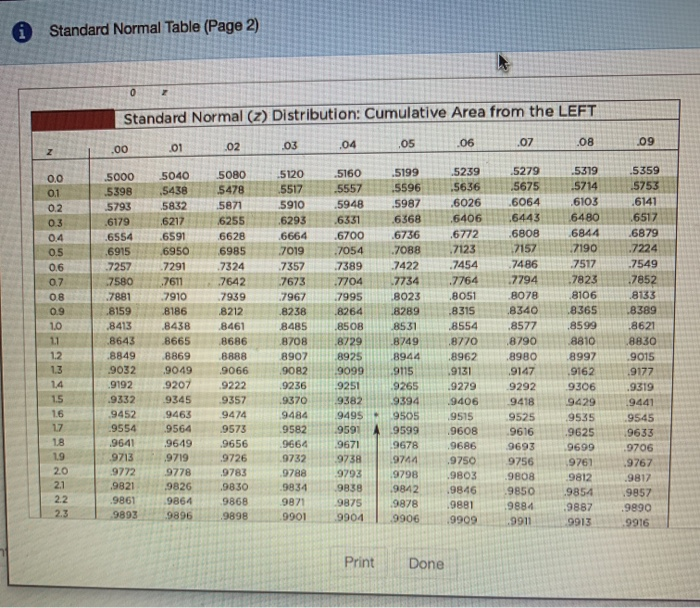
Since the entries in the Standard Normal Cumulative Probability Table represent the probabilities and they are four-decimal-place numbers, we shall write 0.1 as 0.1000 to remind ourselves that it corresponds to the inside entry of the table. The question is asking for a value to the left of which has an area of 0.1 under the standard normal curve. To find the probability between these two values, subtract the probability of less than 2 from the probability of less than 3.


 0 kommentar(er)
0 kommentar(er)
